Πρόβλημα των τριών σωμάτων: Μη πλήρως επιλύσιμο, αλλά συνεχίζει να δίνει ώθηση στα μαθηματικά
Συνήθως η ολοκληρωμένη επίλυση ενός προβλήματος στα μαθηματικά ανοίγει δρόμους για την επίλυση και άλλων προβλημάτων, για νέες ανακαλύψεις. Όμως, υπάρχουν προβλήματα που έχει αποδειχτεί ότι είναι μη πλήρως επιλύσιμα (δεν μπορούν να βρεθούν όλες οι λύσεις τους). Είναι δυνατόν ένα τέτοιο πρόβλημα να βοηθά στην πρόοδο τόσο των ίδιων των μαθηματικών, όσο και των άλλων επιστημών, οι οποίες τα χρησιμοποιούν για την επίλυση των δικών τους προβλημάτων; Ο μαθηματικός γρίφος που ονομάστηκε «πρόβλημα των τριών σωμάτων», ένα μη πλήρως επιλύσιμο πρόβλημα, αποδεικνύει πάλι και πάλι στην ιστορική εξέλιξη της μαθηματικής επιστήμης ότι κάτι τέτοιο είναι πράγματι δυνατό.
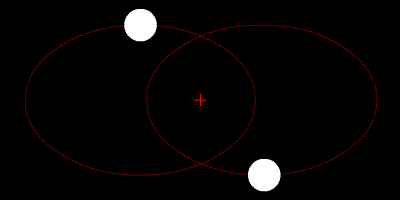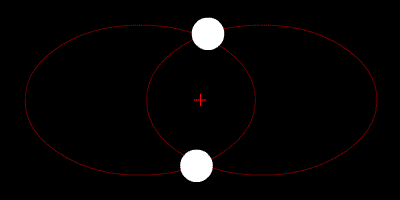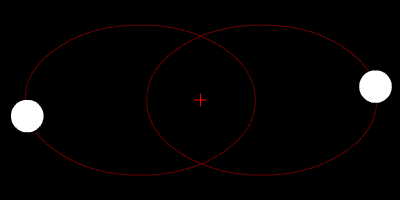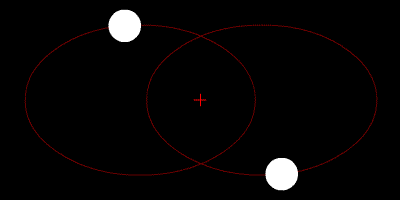 To πρόβλημα των δύο σωμάτων (Φωτό: Public Domain)
To πρόβλημα των δύο σωμάτων (Φωτό: Public Domain)
Το «πρόβλημα των τριών σωμάτων» πάει πολύ πίσω στο χρόνο. Ο Ισαάκ Νεύτων αρχικά διατύπωσε και έλυσε το πρόβλημα των δύο σωμάτων, στην περίφημη δημοσίευσή του «Principia», το 1687. Αναρωτήθηκε: «Πώς θα κινηθούν δύο μάζες στο χώρο αν η μόνη δύναμη που ασκείται πάνω τους είναι η μεταξύ τους βαρυτική έλξη;» Ο Νεύτων μορφοποίησε το ερώτημα ως πρόβλημα επίλυσης ενός συστήματος διαφορικών εξισώσεων, που προσδιορίζουν την κίνηση ενός αντικειμένου, με βάση την τρέχουσα θέση και ταχύτητά του. Το σύστημα αυτό το έλυσε πλήρως, βρήκε αυτό που λέγεται στα μαθηματικά: αναλυτική λύση. Στην ουσία οι λύσεις, που αποκαλούνται και τροχιές, προβλέπουν ότι τα δύο σώματα θα κινούνται σε κωνικές τομές (καμπύλες που προκύπτουν ως τομές ενός επιπέδου και ενός κώνου), δηλαδή κύκλο, έλλειψη, παραβολή ή υπερβολή.
Οι λύσεις που βρήκε ο Καρλές Σιμό στο πρόβλημα των Ν-σωμάτων ίσης μάζας, τις οποίες αποκάλεσε «χορογραφίες», καθώς τα σώματα (4 στη συγκεκριμένη εικόνα) κάνουν συνεχώς έναν περίπλοκο «χορό» το ένα γύρω από το άλλο
Κωνικές
Προσπαθώντας να βρει όλες τις δυνατές λύσεις, ο Νεύτων παρήγαγε μαθηματικά τους εμπειρικούς νόμους για την κίνηση των πλανητών που είχε ανακαλύψει το 1609 ο Γιοχάνες Κέπλερ, βασισμένος στις αστρονομικές παρατηρήσεις δεκαετιών, που έκανε ένας άλλος μεγάλος αστρονόμος, ο μαθητής του Τίχο Μπράχε. Ο πρώτος νόμος του Κέπλερ λέει ότι κάθε πλανήτης (ή κομήτης) κινείται σε μια κωνική τομή, με τον Ηλιο ως εστία της καμπύλης. Ωστόσο, στις λύσεις που έδωσε ο Νεύτων, τα δύο σώματα – ο Ήλιος και ο πλανήτης – κινούνται και τα δύο στη δική τους κωνική. Αυτές οι κωνικές έχουν μια κοινή εστία, που δεν είναι άλλη από το κέντρο μάζας των δύο σωμάτων. Ο Ήλιος έχει πολύ μεγαλύτερη μάζα και όγκο συγκριτικά με κάθε πλανήτη, σε τέτοιο βαθμό μάλιστα, που το κέντρο μάζας του συστήματος Ήλιου – πλανήτη βρίσκεται μέσα στον Ήλιο, πολύ κοντά στο δικό του κέντρο μάζας, με το κέντρο μάζας του Ήλιου απλώς να ταλαντεύεται γύρω από το κοινό κέντρο μάζας, σε μια μικροσκοπική ελλειπτική τροχιά.
Αν στη θέση των δύο μαζών βάλουμε τρεις, τότε προκύπτει το πρόβλημα των τριών σωμάτων. Όπως και στην περίπτωση του προκατόχου του, οι τροχιές είναι λύσεις ενός συστήματος διαφορικών εξισώσεων. Σε αντίθεση, όμως, με το πρόβλημα δύο σωμάτων, είναι δύσκολο έως ακατόρθωτο να βρεθούν ακριβείς μαθηματικοί τύποι για τις τροχιές. Μέχρι σήμερα, παρά την ύπαρξη των σύγχρονων ηλεκτρονικών υπολογιστών και αιώνων ολόκληρων δουλειάς από μερικούς από τους καλύτερους φυσικούς και μαθηματικούς, έχουμε ανακαλύψει μόλις πέντε οικογένειες τροχιών: τρεις που βρήκε ο Λέοναρντ Οϊλερ, το 1767 και δύο που διατύπωσε ο Ζοζέφ – Λουί Λαγκράνζ, το 1772. Το 1890 ο Ανρί Πουανκαρέ ανακάλυψε την ύπαρξη χαοτικής δυναμικής εγγενούς στο πρόβλημα των τριών σωμάτων, εύρημα που σημαίνει ότι δεν θα μπορέσουμε ποτέ να μάθουμε όλες τις δυνατές λύσεις στο πρόβλημα αυτό, σε επίπεδο ακρίβειας, που έστω να προσεγγίζει στην πλήρη λύση του προβλήματος των δύο σωμάτων από τον Νεύτωνα.
Ανικανοποίητοι
Ωστόσο, μέσα από μια διαδικασία που αποκαλείται αριθμητική ολοκλήρωση και γίνεται αποτελεσματικά σε υπολογιστή, μπορούμε να παράξουμε συγκεκριμένα τμήματα τροχιών με ικανοποιητική ακρίβεια, διαδικασία που είναι κρίσιμη για τον σχεδιασμό και την πραγματοποίηση διαστημικών αποστολών στο βαθύ Διάστημα. Επιμηκύνοντας τον διαθέσιμο χρόνο υπολογισμών, μπορούμε να κάνουμε τις προσεγγίσεις όσο ακριβείς θέλουμε. Χάρη σε αυτές τις αριθμητικές μεθόδους επίλυσης προβλημάτων σε υπολογιστή, μπορούν οι διαστημοσυσκευές μας να συναντούν προγραμματισμένα ουράνια σώματα που απέχουν πολλές εκατοντάδες εκατομμύρια χιλιόμετρα απ΄ τη Γη, έχοντας κάνει πολύπλοκες διαδρομές πολλαπλάσιου μήκους μέσα στο ηλιακό σύστημα.
Μπορεί η NASA να ικανοποιείται με τις προσεγγίσεις των λύσεων στο «πρόβλημα των τριών σωμάτων», αλλά δεν συμβαίνει το ίδιο με τους μαθηματικούς, οι οποίοι συνέχισαν και συνεχίζουν να αναζητούν κι άλλες οικογένειες ακριβών λύσεων. Έτσι το 1993, ο Κρις Μουρ, χρησιμοποιώντας αριθμητικές μεθόδους και το 2000 με αναλυτικό τρόπο ο Αλέν Σενσινέρ και ο Ρίτσαρντ Μοντγκόμερι ανακάλυψαν την πρώτη γνωστή περιοδική λύση στο πρόβλημα των τριών σωμάτων, για την περίπτωση που έχουν και τα τρία την ίδια μάζα, οπότε κινούνται πάνω σε ένα επίπεδο, ακολουθώντας τροχιά σχήματος 8, κυνηγώντας το ένα το άλλο, χωρίς ποτέ να συγκρούονται. Η γνωστοποίηση αυτής της ανακάλυψης οδήγησε τον Κάρλες Σιμό να ανακαλύψει εκατοντάδες τροχιές για το γενικότερο πρόβλημα των Ν-σωμάτων ίσης μάζας, τις οποίες ονόμασε «χορογραφίες». Η λύση του σχήματος 8 χρησιμοποιήθηκε μάλιστα και στην τριλογία επιστημονικής φαντασίας «Το Πρόβλημα των Τριών Σωμάτων» του Κινέζου Λιου Σιξίν, που πήρε το 2015 το βραβείο Χιούγκο, αντίστοιχο του Νόμπελ Λογοτεχνίας στην κατηγορία της επιστημονικής φαντασίας.
Η πρώτη περιοδική λύση στο πρόβλημα των τριών σωμάτων, που ανακάλυψαν οι Μουρ, Σενσινέρ και Μοντγκόμερι. Τα τρία σώματα ίσης μάζας κινούνται πάνω σε τροχιά σχήματος 8, κυνηγώντας το ένα το άλλο χωρίς να συγκρούονται
Οι μαθηματικοί που ασχολούνται με το «πρόβλημα των τριών σωμάτων», άνθρωποι με υπομονή και επιμονή, γνωρίζουν ότι δεν βρίσκονται πιο κοντά στην επίλυσή του με τη συμβατική έννοια, αλλά στο μεταξύ έχουν μάθει πολλά. Το πρόβλημα αυτό συνδέει τρεις κλάδους των μαθηματικών: Την τοπολογία, τη γεωμετρία και τη δυναμική και η αναζήτηση λύσεων οδηγεί σε προόδους και στους τρεις. Αρκετή από τη νέα γνώση δεν έχει βρει ακόμη εφαρμογή. Αυτό όμως είναι συχνό φαινόμενο στα σύγχρονα μαθηματικά, όπου αφηρημένες έννοιες και δυσνόητα θεωρήματα αναπτύσσονται καιρό πριν κάποιος βρει πρακτική χρήση γι΄ αυτά.
Επιμέλεια: Σταύρος ΞΕΝΙΚΟΥΔΑΚΗΣ – Πηγή: «Scientific American»
(Αναδημοσίευση από τον Ριζοσπάστη του Σαββατοκύριακου 25-26 Γενάρη 2019)